¿Cómo resolver una ecuación? Baldor te explica 

Todos nos preguntamos que para qué nos enseñan álgebra en la escuela y apoyamos la pregunta diciendo: “Eso nunca lo uso en la vida diaria”. pero eso es un error.   

Un ejemplo del álgebra diaria es éste: fui al mercado y compré dos kilos de calabacitas y un kilo de pimientos que me costó 35 pesos. Pagué por todo 85 pesos creyendo que iba a pagar 75. ¿Cuánto cuesta cada kilo de calabacitas? ¿me timó el vendedor? Es un ejemplo sencillo, pero en la vida hay mucha más álgebra de la que imaginamos. 

Los profesores, el álgebra y el Baldor 

Siempre he comentado que la culpa es de los profesores que no se enteran de lo que pasa en la mente de sus alumnos, que hay que ir de lo más sencillo a lo más complicado y ser lo más claro que se pueda para que los demás entiendan. 

 Me toca ver si soy capaz de explicar bien cómo se resuelve una ecuación y trataré de no caer en lo que tanto denuncio. Pues aquí voy, con ayuda de Baldor. 

Primer paso 

Escojo una ecuación que tiene los elementos necesarios para que ni sea tan obvia la respuesta ni sea tan complicada que ya no permita al lector seguirme el paso: 

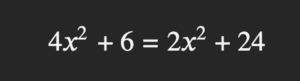
Lo primero que debemos hacer es colocar a todos los términos con incógnitas del lado izquierdo del signo igual y a las cantidades conocidas al lado derecho del signo igual. 

Una de las principales reglas que no debemos olvidar es que al parar un término al lado contrario del signo igual miremos la operación que hace en su lado para que al pasar ese término al lado contrario, lo coloquemos con la operación contraria. 

Segundo paso 

Aquí va: 

El primer término con incógnita, el 4x a la 2, ya está a la izquierda, entonces se pasa el 2x a la 2, que está a la derecha del signo igual, al lado izquierdo: 

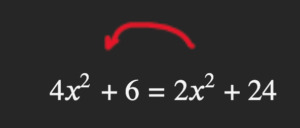
y como está sumando, se pasa restando: 

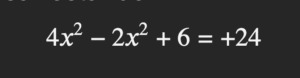
Ahora es necesario pasar el término conocido +6, que está a la izquierda del signo igual al lado derecho:

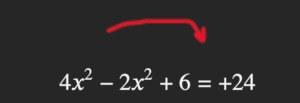
y se le cambia la operación: como estaba sumando, se pasa restando. El término +24 se queda en la derecha, ése es su lugar:

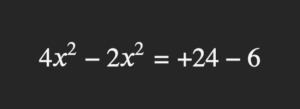
Tercer paso 

En estas condiciones ya se pueden realizar algunas operaciones: si tengo cuatro x cuadradas y le quito dos x cuadradas, quedan solamente dos x cuadradas: 

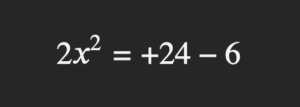
También se puede hacer algo en el lado derecho del signo igual: tengo 24 y le resto 6, el resultado es 18: 

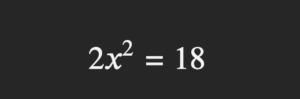
Buena parte de la ecuación está resuelta, ahora trataremos de que la x se quede sola en el lado izquierdo, así que hay que pasar el coeficiente 2 y el exponente 2 (exponente es el 2 pequeñito arriba a la derecha de la x) a la derecha del signo igual. 

Cuarto paso 

¿Cuál debemos pasar primero? ¿el coeficiente o el exponente? Un sencillo análisis nos permite tomar la decisión: el coeficiente 2 es un número que afecta al resto de la expresión, pues ése dice: el doble de la x cuadrada.

Mientras que el exponente 2, el pequeñito, solamente afecta a la x, pues señala: la x se eleva al cuadrado. ¡la x sola! No se eleva al cuadrado al termino 2x… bueno, lo aclaro: si se quisiera elevar al cuadrado al término 2x se debería escribir así: 2x a la 2, pues el paréntesis dice: ¡a todo! 

Aclarado lo anterior, se debe seleccionar el término que afecta a todo, es decir el coeficiente 2:

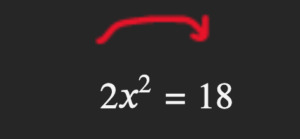
Y como está multiplicando, se pasa dividiendo: 

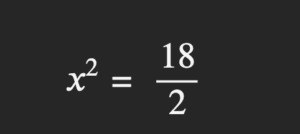
Como la división 18 entre 2 puede hacerse, queda así el resultado: 

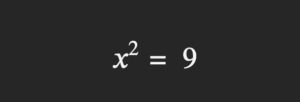
Queda por pasar ese 2 pequeñito, el exponente al lado derecho del signo igual. Como expresa una potencia (al cuadrado), se pasa como una raíz (cuadrada), que es la operación contraria:

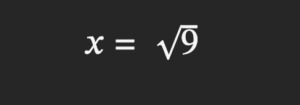
Como la raíz cuadrada de nueve es tres, la ecuación queda resuelta: 

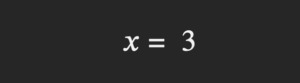
Las matemáticas en realidad son sencillas, los complicados son los profesores, alguno me estará leyendo…  

La explicación y el traje 

Creo que mi explicación es sencilla, pero si alguien no entendió, no es su culpa sino la mía. Una buena explicación matemática es como vender un buen traje: debe hacerse justo a la medida del consumidor y yo, que no me he comunicado eficazmente con los lectores para conocer cuáles son los antecedentes matemáticos que ya tienen, no he ajustado mis palabras a sus necesidades.  

Por: Gabriel Calderón